Level curve definition, contour line See more The height of the tower from the level of the street is 105 feet, the slated towers over the lateral pediments being smallerView sea level rise and potential coastal flooding impact areas and relative depth The data and maps in this tool illustrate the scale of potential flooding, not the exact location, and do not account for erosion, subsidence, or future construction Water levels are relative to Mean Higher High Water (MHHW) (excludes wind driven tides)Level curves for a function the level curve of value is the curve in on which Notice the critical difference between a level curve of value and the trace on the plane a level curve always lies in the plane, and is the set of points in the plane on which , whereas the trace lies in the plane , and is the set of points with in By combining the level curves for equally spaced values of into one

Level Sets Math Insight
Level curves
Level curves-The level curves for {eq}k=1,2,3,4,5 {/eq} are shown below Become a member and unlock all Study Answers Try it riskfree for 30 days Try it riskfree Ask a question Our experts can answer yourThe level curves in this case are just going to be lines So, for instance, if we take the level curve at z equals 0, then we have just the equation 2x plus y equals 0 And so that has intercept so we're looking at so 0 equals 2x plus y, so that's just y equals minus 2x So that's this level curve




Level Curves
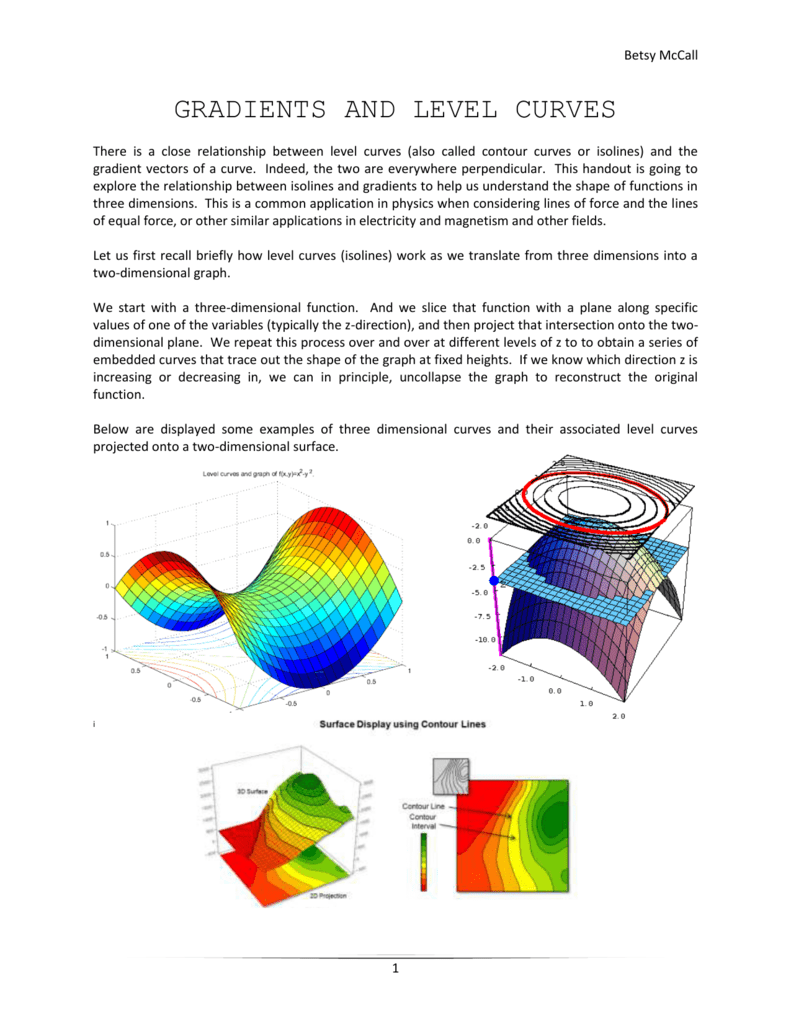
Ie the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the functionGRADIENTS AND LEVEL CURVES There is a close relationship between level curves (also called contour curves or isolines) and the gradient vectors of a curve Indeed, the two are everywhere perpendicular This handout is going to explore the relationship between isolines and gradients to help us understand the shape of functions inExample 1 Let f ( x, y) = x 2 − y 2 We will study the level curves c = x 2 − y 2 First, look at the case c = 0 The level curve equation x 2 − y 2 = 0 factors to ( x − y) ( x y) = 0 This equation is satisfied if either y = x or y = − x Both these are equations for lines, so the level curve for c = 0 is two lines If you
LEVEL CURVES The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant; Mathematica has a builtin command to generate plots of the level curves of a function f of two variables The basic form of the command is where F x, y is an expression in the variables x and y, which range over the respective intervals xmin, xmax and ymin, ymax For the function f with formula f (x, y) = , with x and y eachPurpose To determine serum insulinlike growth factor 1 (IGFI) levels in healthy Chinese adults, establish reference ranges for serum IGFI levels and observe the effects of age, sex, body mass index (BMI) and geographical region on serum IGFI levels Methods In total, 2791 healthy adults (1339 males and 1452 females) from the north (Beijing) and south (Guizhou Province) of China
If you're working with some other 3D graph then, you'll want to check to find which values of x and y together produce z The easiest way to do this is to set a fixed value for one variable and then solve for the other So, if you have a function F (x,y) = 2x 3y, and you want to create a contour line for z = 3We have locations around the world!Level Curves This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both and




How To Draw Level Curves For X X 2 Y 2 Mathematics Stack Exchange



Contour Lines Rodolphe Vaillant S Homepage
Level curves The two main ways to visualize functions of two variables is via graphs and level curves Both were introduced in an earlier learning module For your convenience, that learning module page is reproduced hereFree ebook http//tinyurlcom/EngMathYT How to sketch level curves and their relationship with surfaces Such ideas are seen in university mathematics andPractice problems Sketch the level curves of Sketch the threedimensional surface and level curves of Consider the surface At , find a 3d tangent vector that points in the direction of steepest ascent Find a normal vector to the surface at the point Give the equation for the tangent plane to the surface at the point



Example Contour Plots Or Level Curves




Calculus Iii Functions Of Several Variables
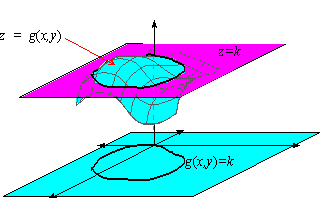
A level curve of f (x, y) is a curve on the domain that satisfies f (x, y) = k It can be viewed as the intersection of the surface z = f (x, y) and the horizontal plane z = k projected onto the domain The following diagrams shows how the level curves f (x, y) = 1 1 − x 2 − y 2 = kLevel curves and the implicit function theorem Differentiation The basic component of severalvariable calculus, twodimensional calculus is vital to mastery of the broader field This extensive treatment of the subject offers the advantage of a thorough integration of linear algebra and materials, which aids readers in the development of geometric intuitionThen the curves obtained by the intersections of the planes $z = k$, $k \in \mathbb{R}$ with the graph of $f$ are called the Level Curves of $f$ From the definition of a level curve above, we see that a level curve is simply a curve of intersection between any plane parallel to the $xy$ axis and the surface generated by the function $z = f(x, y)$




Level Curves
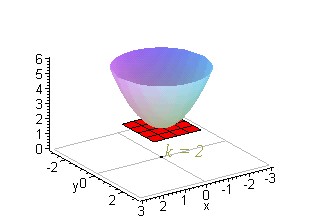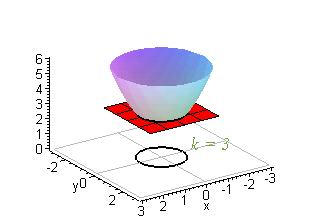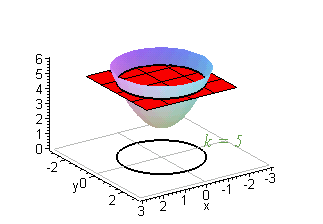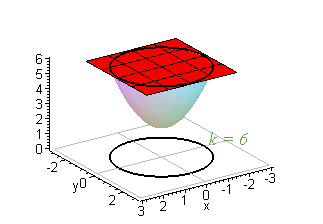



Gradients And Level Curves
The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any number So the equations of the level curves are \(f\left( {x,y} \right) = k\) Note that sometimes the equation will be in the form \(f\left( {x,y,z} \right) = 0\) and in these cases the equations of the level curves are \(f\left( {x,y,k} \right) = 0\)Find 7 ways to say LEVEL CURVE, along with antonyms, related words, and example sentences at Thesauruscom, the world's most trusted free thesaurus Level Curve A level set in two dimensions Phase curves are sometimes also known as level curves (Tabor 19, p 14) SEE ALSO Contour Plot, Equipotential Curve, Level Surface, Phase Curve REFERENCES Tabor, M Chaos and Integrability in Nonlinear Dynamics An Introduction New York Wiley, 19



Relief Functions And Level Curves
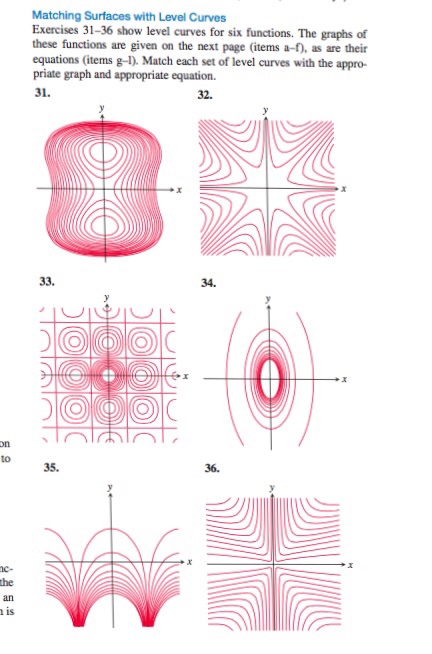



Matching Surfaces With Level Curves Exercises 31 36 Chegg Com
Level curves Loading level curves level curves Log InorSign Up x 2 y 2 − z 2 = 1 1 z = − 0 8 2 31 You have a function f R 2 → R The level curves of f is the set { ( x, y) ∈ R 2 f ( x, y) = K, K ∈ R } So, in order to find the level curves of your function, just set it equal to a constant K, and try different values of K For instance f ( x, y) = ( x 2 y 2 − 1) (The level curves (or contour lines) of a surface are paths along which the values of z = f (x,y) are constant;




Level Curves Of The Error Function Download Scientific Diagram
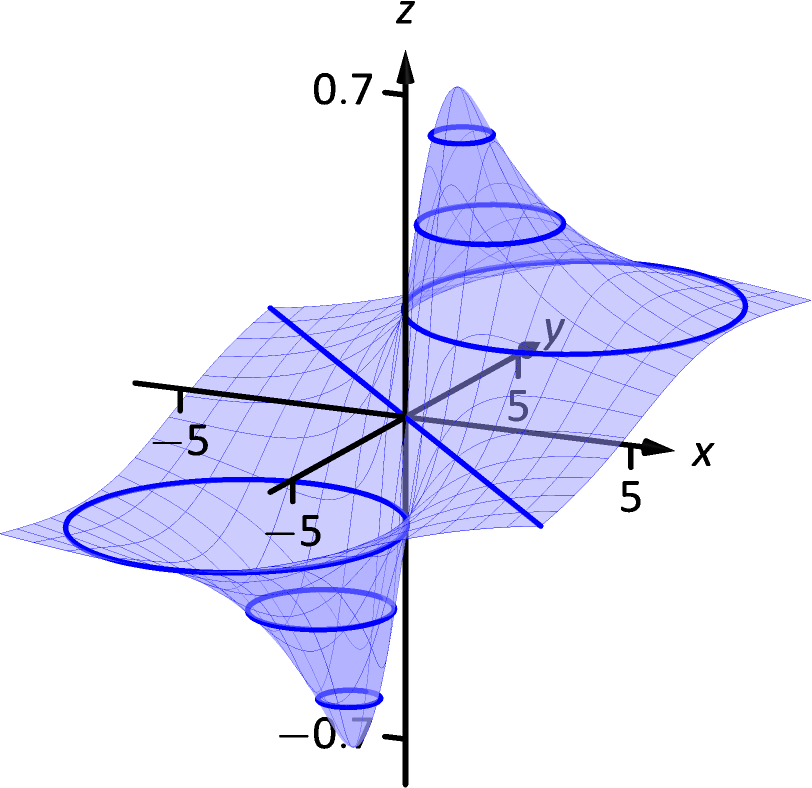



13 1 Introduction To Multivariable Functions Chapter 13 Functions Of Several Variables Part Calculus Iii
Ie the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is This will give us the sketch of level curves of the function In this video we're going to talk about how to find the level curves both graphically (by looking at a picture of the threedimensional figure) and algebraically, by replacing z in the multivariable function with a constant c, and then substituting different values for c in order toLevel Curves In mathematics, a level set of a realvalued function f of n real variables is a set where the function takes on a given constant value c




Level Curves Of Functions Of Two Variables Youtube




Math 15 Lecture 7 Level Curves And Contour Plots Oneclass
A level curve of a function f (x, y) is the curve of points (x, y) where f (x, y) is some constant value A level curve is simply a cross section of the graph of z = f (x, y) taken at a constant value, say z = c A function has many level curves, as one obtains a different level curve for each value of c in the range of f (x, y)Solution First, let z be equal to k, to get f (x,y) = k Secondly, we get the level curves, or Notice that for k >0 describes a family of ellipses with semiaxes and Finally, by variating the values of k, we get graph bellow (Figure 3), called, level curves or contour map Firgure 3 Level curves of fSolution The level curves of are curves in the plane along which has a constant value We now sketch the resulting curves for a couple values of The curve consists of all points satisfying That is, it has points where or Similarly, the and level curves are given by and Hence our sketch of the level curves of looks like




Visualizing Surface And Level Curves Youtube




Level Curves
Level Curves and Cross Sections Main Concept A level curve of the surface is a twodimensional curve with the equation , where k is a constant in the range of f A level curve can be described as the intersection of the horizontal plane with the surface A level curve of a function f(x,y) is the curve of points (x,y) where f(x,y) is some constant value A level curve is simply a cross section of the graph of z=f(x,y) taken at a constant value, say z=c A function has many level curves, as one obtains a different level curve for each value of c in the range of f(x,y)Level Curves In this activity we will introduce Matplotlib's contour command, which is used to plot the level curves of a multivariable function Let's begin with a short discussion of the level curve concept Hikers and backpackers are likely to take along a copy of a topographical map when verturing into the wilderness (see Figure 1)




Level Curve From Wolfram Mathworld




Level Set Wikipedia
A level curve of a function f(x,y) is a set of points (x,y) in the plane such that f(x,y)=c for a fixed value c Example 5 The level curves of f(x,y) = x 2 y 2 are curves of the form x 2 y 2 =c for different choices of c These are circles ofVisit Curves to find a women's fitness club near you Simply enter your city and state, or postal code, and we'll provide you with information on your nearby Curves gyms Find out more!The level curves of f(x,y) are curves in the xyplane along which f has a constant value
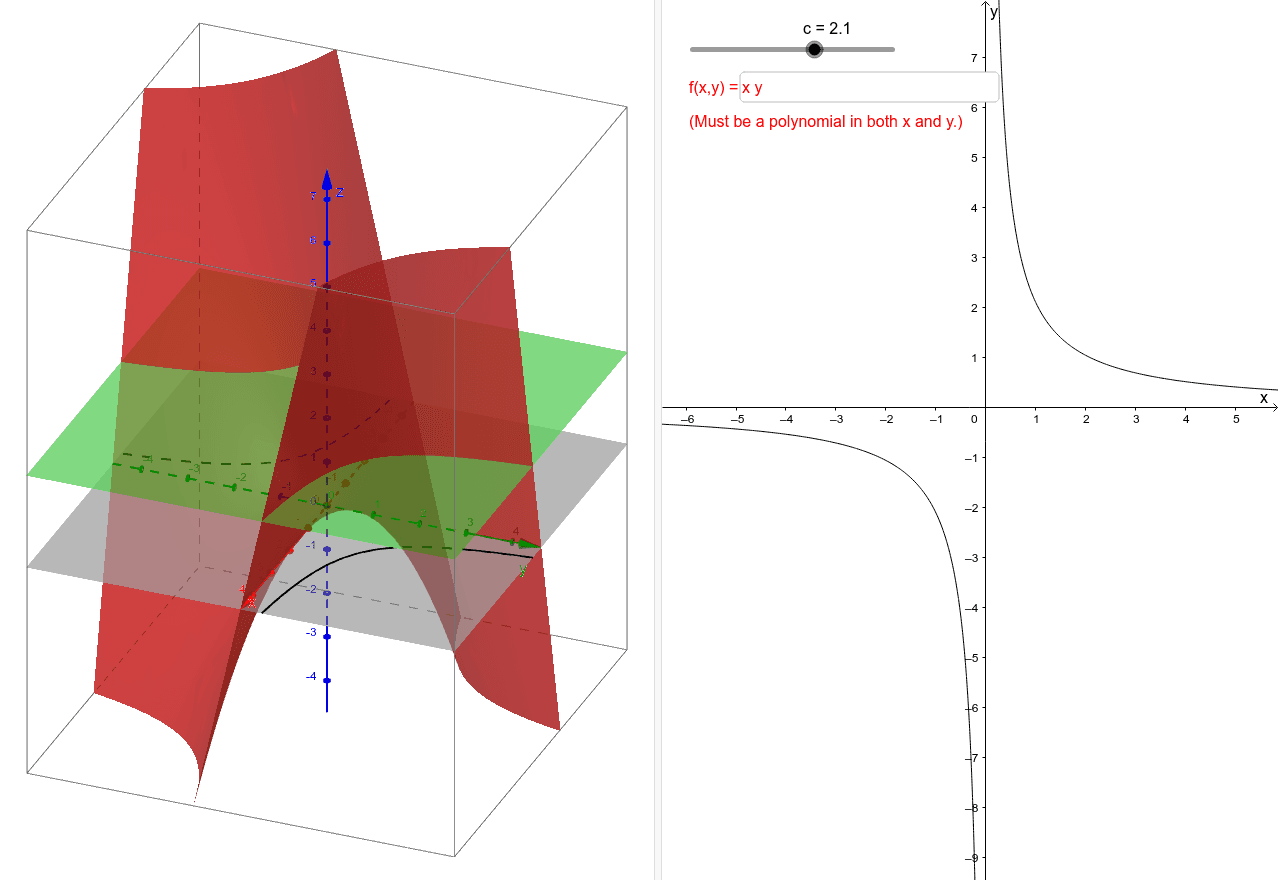



Level Curves Geogebra
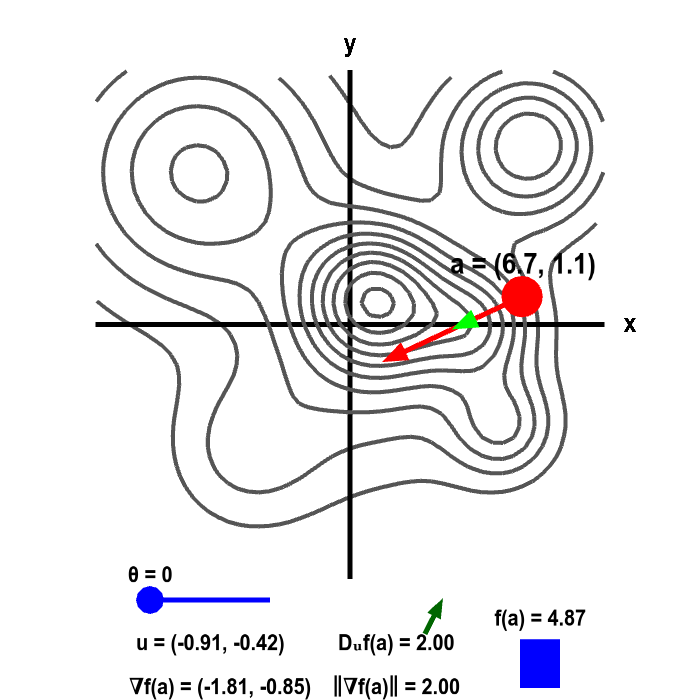



Applet Gradient And Directional Derivative On A Mountain Shown As Level Curves Math Insight
2 Screw the level onto the tripod On the underside of the level are four leveling screws Each screw should be touching the plate at the top of the tripod If not, extend the leveling screws until they all touch the plate (Figure 6) 1 Adjust the level by turning the telescopic sight to align with opposite pairs of screws 2 Turn the screws Level curves Author Siamak The level curves of two functions and Blue represents and red represents Since and are both harmonic and is a harmonic conjugate of , the level curves of and intersect each other at right anglesLevel Curve Grapher Level Curve Grapher Enter a function f (x,y) Enter a value of c Enter a value of c Enter a value of c Enter a value of c




How To Sketch Level Curves Vector Calculus Youtube




Gradients And Level Curves
Gradient is perpendicular to the level curves) Note, this problem is strictly about 2D functions w = f(x, y) and their gradients and level curves Also note, for Answer Suppose w = f(x, y) and we have a level curve f(x, y) = c Implicitly this gives a The following image shows level curves of some function \z=f(x,y)\ I need to determine whether the following partial derivatives are positive or negative at the point P \f_{x} , f_{y} , f_{xx} , f_{yy} , f_{xy} , f_{yx}\ I am not sure how to relate the partial derivatives to the level curves I know that partial derivatives at a pointSection 56 Level Surfaces Video Here is a short video about Level Surfaces in CalcPlot3D created by Professor Larry Green of Lake Tahoe Community College It is difficult to draw many interesting level surfaces by hand, but CalcPlot3D helps us explore them easily There are actually two ways to enter and graph the level surface equations for a particular function of three variables in




16 1 Functions Of Several Variables
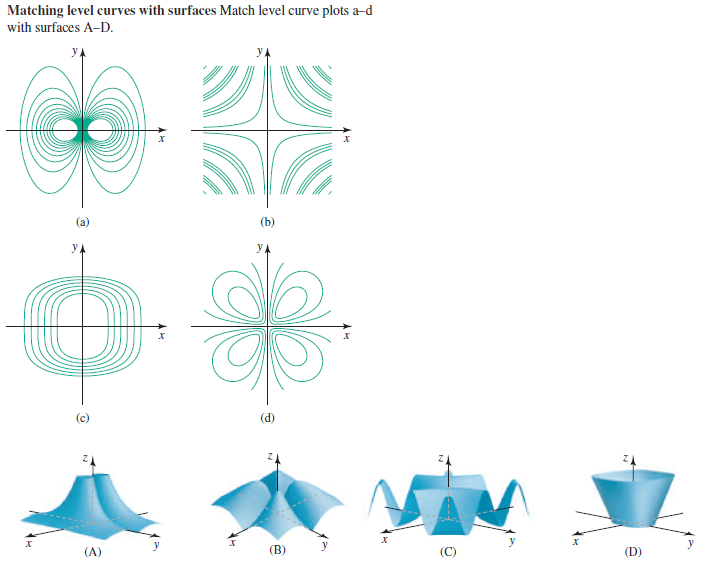



Answered Matching Level Curves With Surfaces Bartleby
Blizzard has recapped how the Great Vault loot will work at the start of Season 2, and has also posted some item level curve adjustments for Mythic rewards A Mythic15 or higher is required to get the maximum item level from the Great Vault, while Mythic14 or higher provides the highest endofrun item levelLevel sets show up in many applications, often under different names For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit equationAnalogously, a level surface is sometimes called an implicit surface or an isosurface The name isocontour is also used, which means a contour ofLike finding level curves for this $$ z=e^{x^2y^2}$$ Thanks in advance calculus graphingfunctions Share Cite Follow asked Nov 27 '14 at 53 João Pedro João Pedro 650 7 7 silver badges 23 23 bronze badges $\endgroup$ 2




Level Curves Mit 18 02sc Multivariable Calculus Fall 10 Youtube




Describe The Level Curves Of The Function Z 8 2x 7y Chegg Com
curve direct Curve direct is a software intended for all people seeking to view the behavior of automatic breaking devices placed in cascade in a LV electrical network Curve direct is used to view coordination between devices This tool therefore enhances the level of continuity of service of an installation Original question Find an equation of the level curve of f(x,y) = yx^2 – y^2 through the point (2,1) and find an equation of the tangent line to the level curve at this point I think I have found the equation of the tangent line to the level curve 10 = 4x 2y (is this correct??), but ILooking for a nearby women's gym?
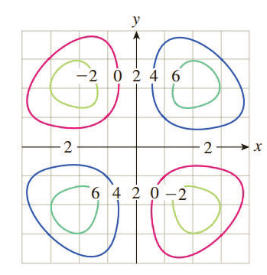



Exercises 55 58 Refer To The Following Plot Of Some Level Curves Of F X Y C For C 2 0 2 4




Surface From Level Curves Of Unkown Levels In Matlab Stack Overflow
A level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of function when equated to some constant values ,example a function of two variables say x and y ,then level curve is the curve of points (x,y) ,where function have constant value Can be better understood by an example



Level Curves And Contour Plots Mathonline




Some Level Curves For The Total Energy E U V The Trajectory That Download Scientific Diagram



Level Sets Ximera




Level Sets Math Insight




Level Curves Curves Level Stvincent Glogster Edu Interactive Multimedia Posters




Level Curves And Implicit Differentiation Studocu



Level Curves Ubc Wiki



Gradients Level Curves




Level Curves In Mathbb R 3 Mathematics Stack Exchange




Sketch The Level Curves Of The Function G X Y Chegg Com




Level Curve And A Surface Tex Latex Stack Exchange




Matlab How Can I Get The Expression Of The Level Curves Of A Function Stack Overflow
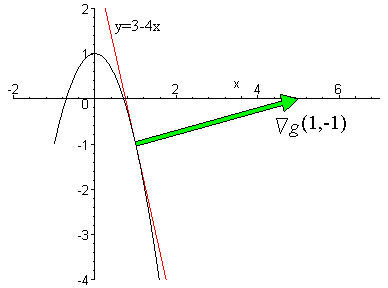



Gradients And Level Curves




Describe The Level Curves Of The Function Z X2 Chegg Com




Level Curves Examples Level Surface




Level Sets Math Insight




Level Curves Calculus




Level Curves




Level Set Wikipedia




Level Curves Are Shown For A Function F Determine Whether The Following Partial Derivatives Are Positive Or Negative At The Point P A F X B F Y C F Xy Study Com



Other Instances Of Level Curves



Level Curves Project Project
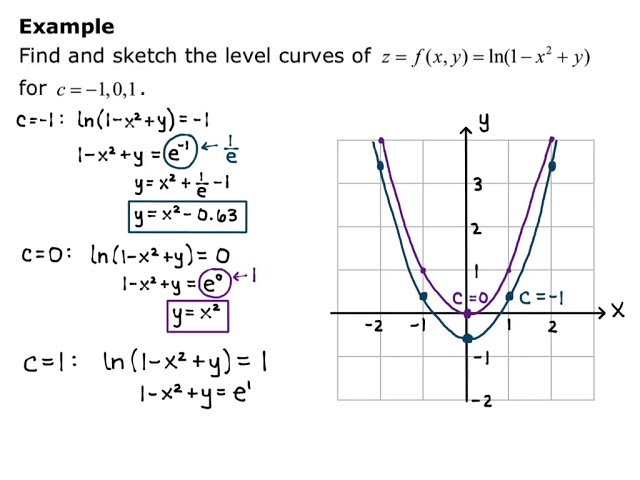



Section 13 1 Level Curves Youtube



Http Math Oregonstate Edu Garity 254h Winter13 Notes 10 Graphs Levelcurves Pdf
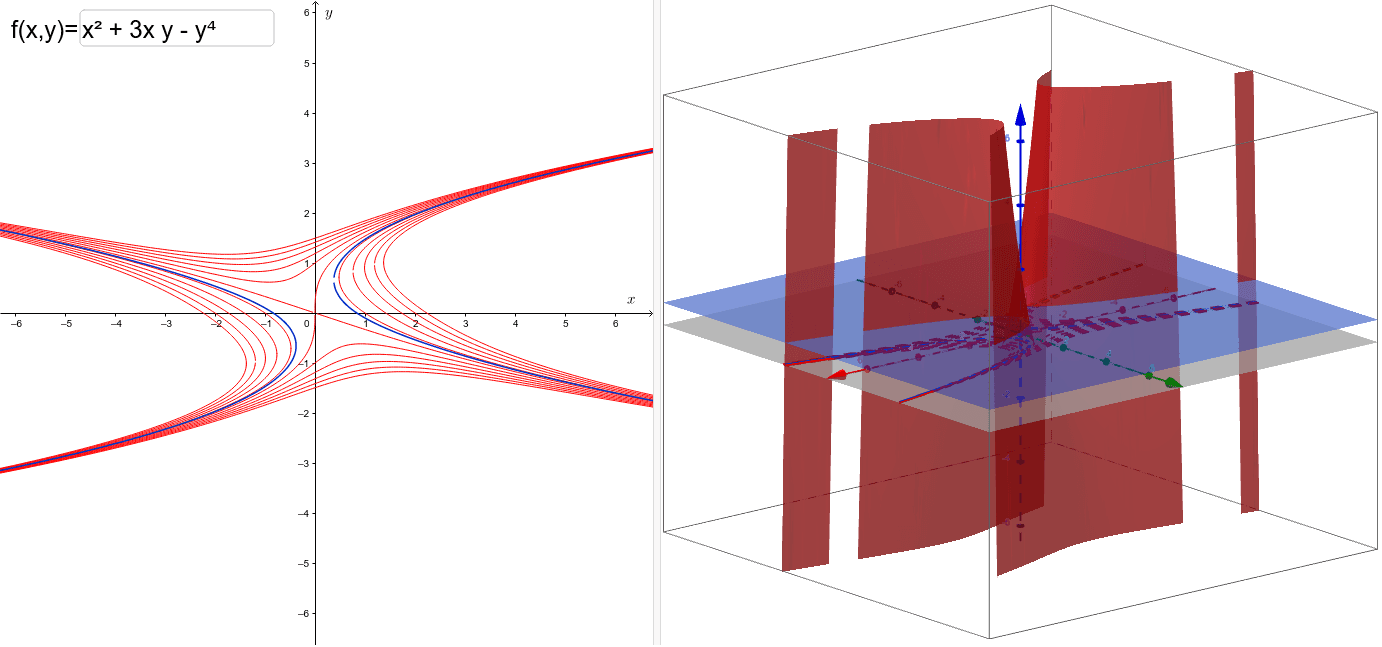



Level Curves Geogebra



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework13 1 Ans Pdf




Calculus Iii Functions Of Several Variables
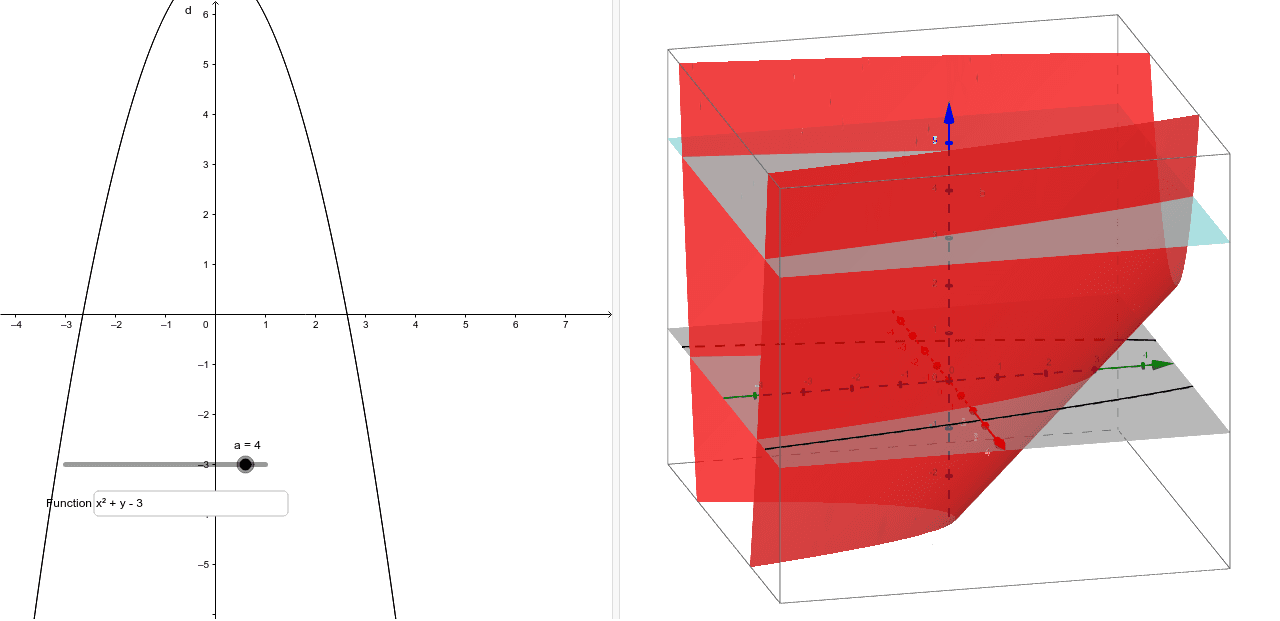



Visualizing Level Curves Geogebra



1




Level Sets Ximera



Problem Of Level Curves Leading Lesson



Gradients And Level Curves




How To Sketch Level Curves Vector Calculus Vector Calculus Calculus Math Notes



Problem On Surfaces And Level Curves Leading Lesson




Level Set Examples Math Insight




A Few Level Curves Of Z F X Y Are Shown A As Accurately As You Can Approximate Bigtriangledown F 2 3 B Use Your Result From Part A To Obtain An Equation




How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 3 Youtube



1



Level Curves And Gradient Vectors In Winplot




Level Set Wikipedia



Level Curves




Level Curves



Www3 Nd Edu Taylor Math550 Images Currentexamsolutions Exam2f16 Pdf



Draw Level Curves For Functions Of Two Variables In C C Helper




Level Curves Of C R R Solid Lines Limiting Curve Labeled Zero Download Scientific Diagram




Session 35 Gradient Definition Perpendicular To Level Curves Part B Chain Rule Gradient And Directional Derivatives 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Level Curves Example 1



Solved The Figure Shows Level Curves Of A Functio




How To Sketch Level Curves Youtube




Graph The Level Curves Of F X Y Frac Y K For K 1 2 4 Study Com




Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube




Problems With Level Curves First Steps Julialang




Schematic Level Curves Of G P Q Values Of Wbow Kernel And The New Download Scientific Diagram



Level Curves Geogebra




Level Curves Geogebra Dynamic Worksheet
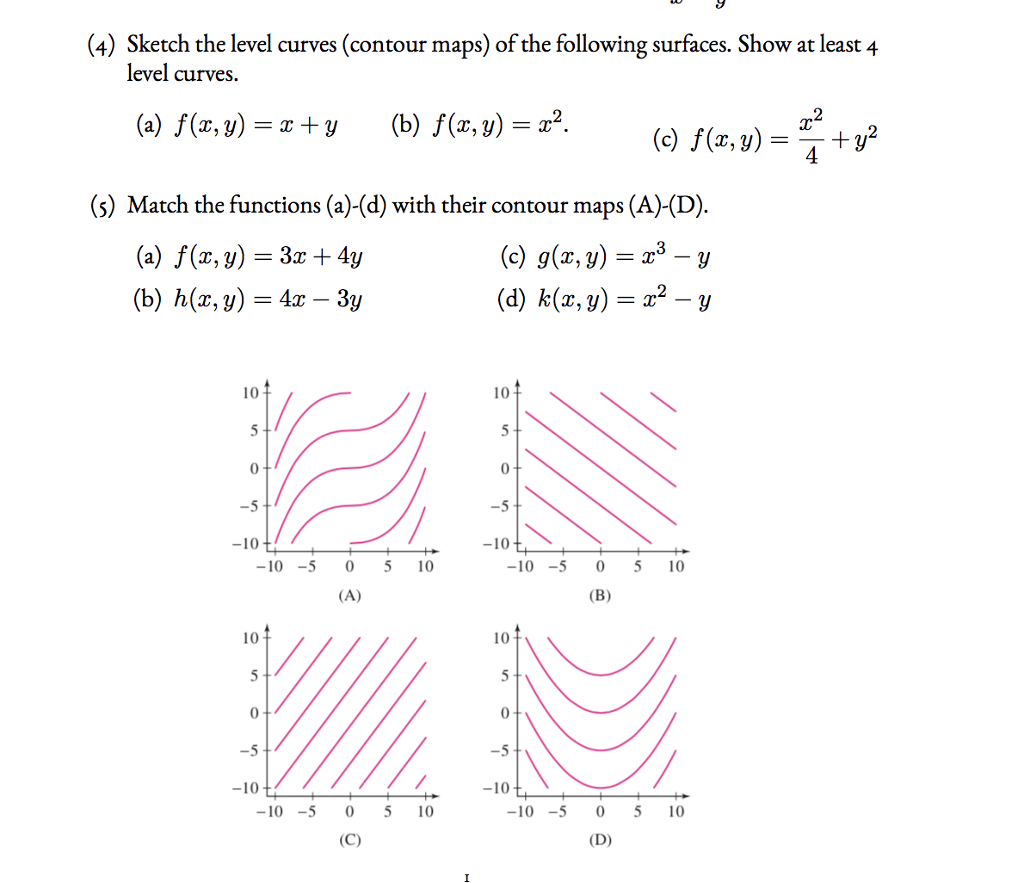



4 Sketch The Level Curves Contour Maps Of The Chegg Com




Contour Maps In Matlab




Partial Derivatives By Level Curves Mathematics Stack Exchange



1




Session 35 Gradient Definition Perpendicular To Level Curves Part B Chain Rule Gradient And Directional Derivatives 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



Mathematics Calculus Iii



Level Sets Ximera



Www Usna Edu Users Math Uhan Sm223 Lessons 12 level curves Pdf



1




Left Level Curves Of Distorted Density F X Y Center Level Download Scientific Diagram




Level Sets Math Insight




Matlab How Can I Get The Expression Of The Level Curves Of A Function Stack Overflow




Solved Example 11 Sketch The Level Curves Of The Function Chegg Com




13 1 Functions Of Several Variables Mathematics Libretexts



Level Curves Physics Forums
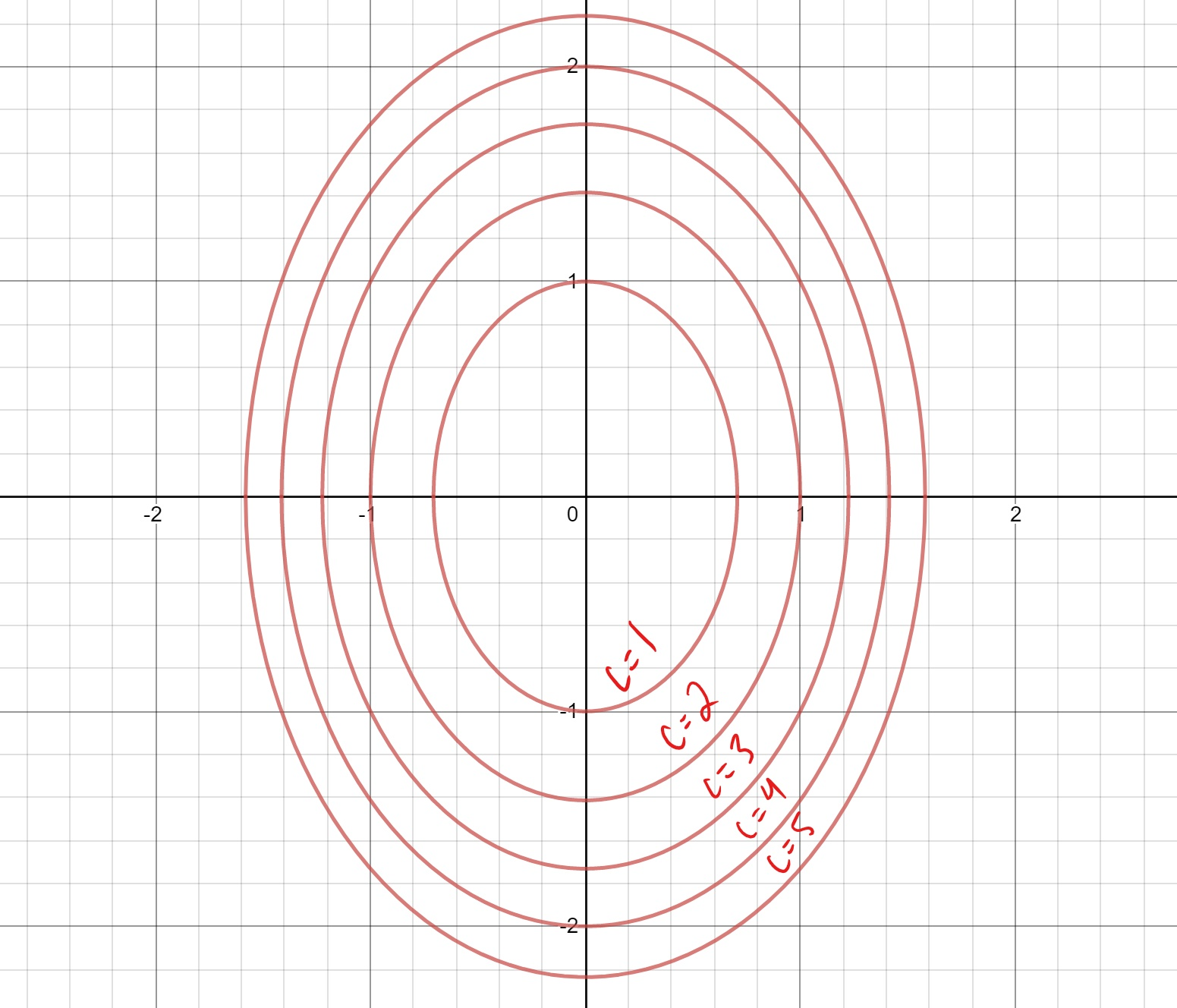



Describe The Level Curves Of The Function Sketch A Contour Map Of The Surface Using Level Curves For The Given C Values Z 2x Y C 1 2 3 4 5 Homework Help And Answers Slader



Contour Lines Rodolphe Vaillant S Homepage



Relief Functions And Level Curves




Graphs And Level Curves




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Level Set Examples Math Insight




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Relation Between Level Curves And Horizontal Traces Tex Latex Stack Exchange



0 件のコメント:
コメントを投稿